円の半径を r r 、同じく球の半径を r r とすると、 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3πr3 V = 4 3 π r 3回転体の断面は必ず円となることから、どちらも 円の面積を積分する計算 になるのですね。 例題「曲線を x 軸周りに回転してできる立体の体積」 それぞれの公式を、例題で確認しましょう。体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう!

中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su
円 体積 公式
円 体積 公式-では実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。円柱の体積を求める公式は、 V = Sh = πr^2 h で表されます。このページでは、例題と共に、円柱の体積を計算する方法を説明しています。また、斜円柱の体積の求め方も説明しています。



どうして1 3なの 錐の体積の公式の求め方 まなべーと
よって、この円の面積は半径×半径×314より 7×7×314=(㎠)となります。 答え ㎠円の接線・弦 ・円の接線は接点を通る半径に垂直である ・円の弦の垂直二等分線は円の中心を通る ・円外の点から円に引いた接線の長さは等しい 接弦定理 ・\( \angle ABT = \angle ACB \) 円に内接する四角形 ・円に内接する四角形の対角の和は\( 180^\circ \)である円柱の体積を求める公式は、 V = Sh = πr^2 h で表されます。このページでは、例題と共に、円柱の体積を計算する方法を説明しています。また、斜円柱の体積の求め方も説明しています。
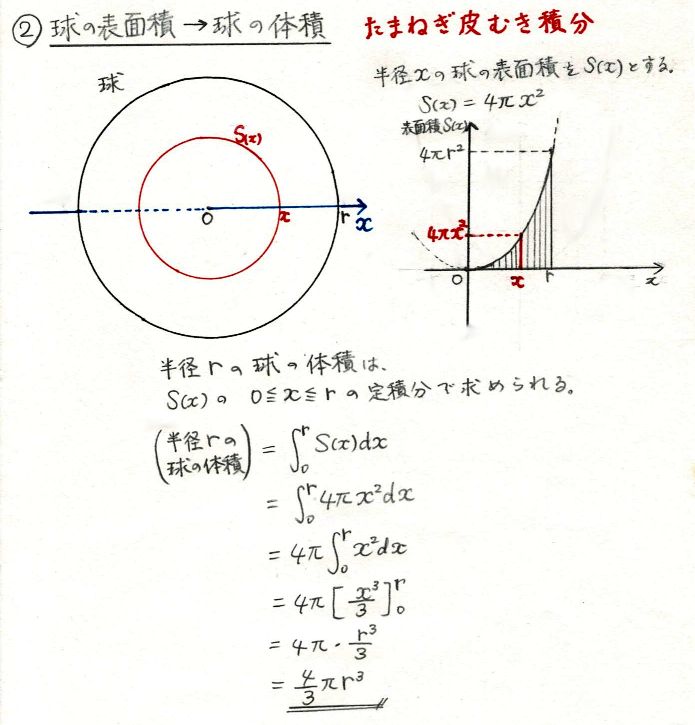
球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) \(\displaystyle \frac {6}{D \rho}\) 半分以上隠れている円の直径の推定 接触角の概算 円と球の空間体積の公式 ・考え方 6 表 と比の公式・考え方 10 水そうの公式・考え方 11 その他の公式・考え方 特集① 12 その他の公式円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式まずは公式を書いておきます。半径を \(r\) として\(V=\displaystyle\frac{4}{3}\p
平面図形 公式集 a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積 四角柱 円の面積 円の周りの長さ(円周)円の面積の公式|「なぜ半径と円周率で求められるのか」を小学生に分かりやすく説明する方法 「なぜ公式で円の面積が計算できるの? 」 小学生のお子さんにうまく説明できずにいる人は多いと思います。円柱の体積の公式 V=πr 2 hって? 円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。 ある円柱において、底面の円の半径を r 、高さを h 、その円柱の体積を V とすると、V=πr 2 h この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率



3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ


球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス
円柱の体積は、 (半径)×(半径)×314 314 ×(高さ) で求めることができます。 円周率を π π 、底面の円の半径を r r 、高さを h h として文字で表すと、その体積 V V は、 V =πr2h V = π r 2 h となります。 底面の半径が r r 、高さが h h の円柱 円柱の体積は小学校で習い、中学校ではそれを π π などの文字を用いて表しますが、どちらにしても体積は、 (底面積の体積を求めることができます。 例えば,右の図のように,半径が2 cmで,中心と直線l との距離が6 cm である円を,直線l のまわりに1回転させてできるドーナツ形の体積は, 円の面積=π×22=4π(cm2), 中心Oがえがく円周の長さ=2π×6=12π(cm)円周長から体積計算 円柱 公式 求め方 バー 棒 高さ 長さ 直径 自動 volume



円柱の表面積と体積を求める公式 具体例で学ぶ数学
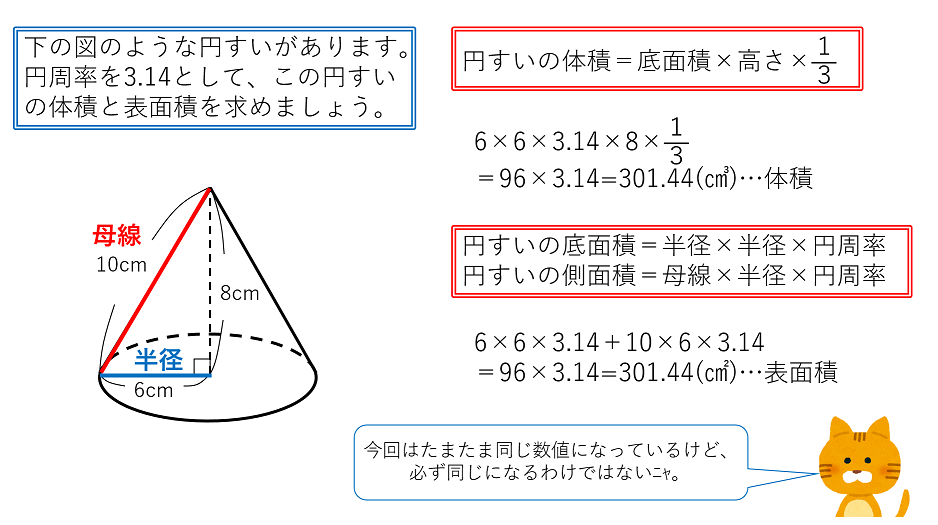


公式を図解 すい体の体積 円すいの表面積の求め方 中学受験ナビ
円周長から体積計算 円柱 公式 求め方 バー 棒 高さ 長さ 直径 自動 volume円柱の体積の解説 円柱の体積を求める公式は 半径×半径×円周率×高さ です。円の面積が 半径×半径×円周率 なので、 円の面積×高さ とも言えます。 円柱の体積を求める公式おうぎ形の弧の長さ = 直径 × 円周率 × 中心角 ÷ 360 扇 形 の 弧 の 長 さ 直 径 円 周 率 中 心 角 扇形の弧の長さ=直径 × 円周率 × 中心角 360



円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ



体積の求め方 計算公式一覧
円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして使用目的 重量計算の際の体積を求めたかったため ご意見・ご感想 中空円の面積の求め方はs=π÷4((外円の直径×外円の直径)(内円の直径×内円の直径))だと思うのですが、中空円柱では÷4が無いのはなぜでしょうか?



円錐の体積の求め方 公式と計算例



円錐の体積ってなんであの公式なの Webty Staff Blog
円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式 まずは公式を書いておきます。 半径を \(r\) として \(V=\displaystyle\frac{4}{3}\pi r^3\) 証明体積の公式 基本的な体積計算の公式をいくつか示す。( π は円周率) 立方体 s 3 (s は一辺の長さ) 直方体 lwh(奥行き l, 幅 w, 高さ h) 円柱 π r 2 h(底円の半径 r, 高さ h) 球 4 / 3 π r 3 (球の半径 r) 円錐 1 / 3 π r 2 h(底円の半径 r, 高さ h)今回は小学校の算数で勉強する、円の面積・円周の求め方について書いていきたいと思います。(年6月日追記しました。) 円周の求め方公式 円の面積の求め方公式 円の面積・円周の長さを求める問題 問題① 《円の面積の求め方》 《円周の長さの求め方》 問題② 《円周の長さの



中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく


ドーナツ形状の体積と表面積
Y = f (x) , x = a , x = b , x 軸で囲まれた領域を x 軸のまわりに回転させてできる図形の体積は, V = ∫ a b π { f (x) } 2 d xDxdydz = abcdudvdw ⋅⋅⋅ (34) d x d y d z = a b c d u d v d w ⋅ ⋅ ⋅ ( 34) だから求めたい体積は、 V = ∫ ∫ ∫ dxdydz = abc∫ ∫ ∫ dudvdw V = ∫ ∫ ∫ d x d y d z = a b c ∫ ∫ ∫ d u d v d w もうここまで来たら、 dudvdw d u d v d w を積分した値は「半径1の球の体積と同じ ( 4 3π13 4 3 π 1 3 )」だから、 V = 4 3πabc ⋅⋅ ⋅(35) V = 4 3 π a b c ⋅ ⋅ ⋅ ( 35) と、公式通りになりました。今回は小学校の算数で勉強する、円の面積・円周の求め方について書いていきたいと思います。(年6月日追記しました。) 円周の求め方公式 円の面積の求め方公式 円の面積・円周の長さを求める問題 問題① 《円の面積の求め方》 《円周の長さの求め方》 問題② 《円周の長さの


地図の体積計測



中学1年生 数学 無料問題集 角柱や円柱の体積 おかわりドリル
円の面積の公式|「なぜ半径と円周率で求められるのか」を小学生に分かりやすく説明する方法 「なぜ公式で円の面積が計算できるの? 」 小学生のお子さんにうまく説明できずにいる人は多いと思います。回転体の断面は必ず円となることから、どちらも 円の面積を積分する計算 になるのですね。 例題「曲線を x 軸周りに回転してできる立体の体積」 それぞれの公式を、例題で確認しましょう。の体積を求めることができます。 例えば,右の図のように,半径が2 cmで,中心と直線l との距離が6 cm である円を,直線l のまわりに1回転させてできるドーナツ形の体積は, 円の面積=π×22=4π(cm2), 中心Oがえがく円周の長さ=2π×6=12π(cm)



円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題



円柱の体積の計算 リットルへの変換も考えてみよう 中学数学 理科の学習まとめサイト



中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



相似な円柱の表面積比 体積比 中学数学 By Okボーイ マナペディア


Math 円柱 内接する球 円錐の体積と表面積 働きアリ



回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学



中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su



簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく


円錐 球 円柱の体積 雑学のソムリエ



円錐の体積を求める Youtube


図のような円錐台の体積を求めるにはどのような計算をすればよいか教えてください Yahoo 知恵袋



球の体積 表面積 無料で使える中学学習プリント



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



数学講師必見 中学数学でも必須 球の体積 表面積の覚え方と導出まとめ 高校数学 塾講師ステーション情報局



中学数学 円柱の体積の求め方と公式 塔をモチーフ なぜか分かる はかせちゃんの怪しい研究室



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ


立体の体積 V 表面積 S または側面積 F および重心位置 G 直円柱 P12



簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円すい 円錐 の体積の求め方と問題 小学数学 Irohabook


研究
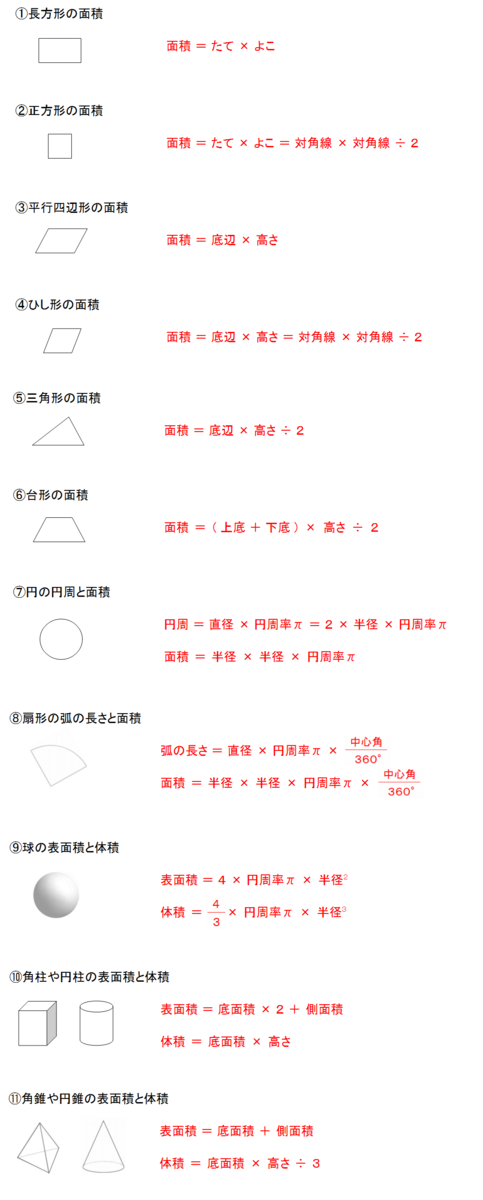


図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師


質量と比重
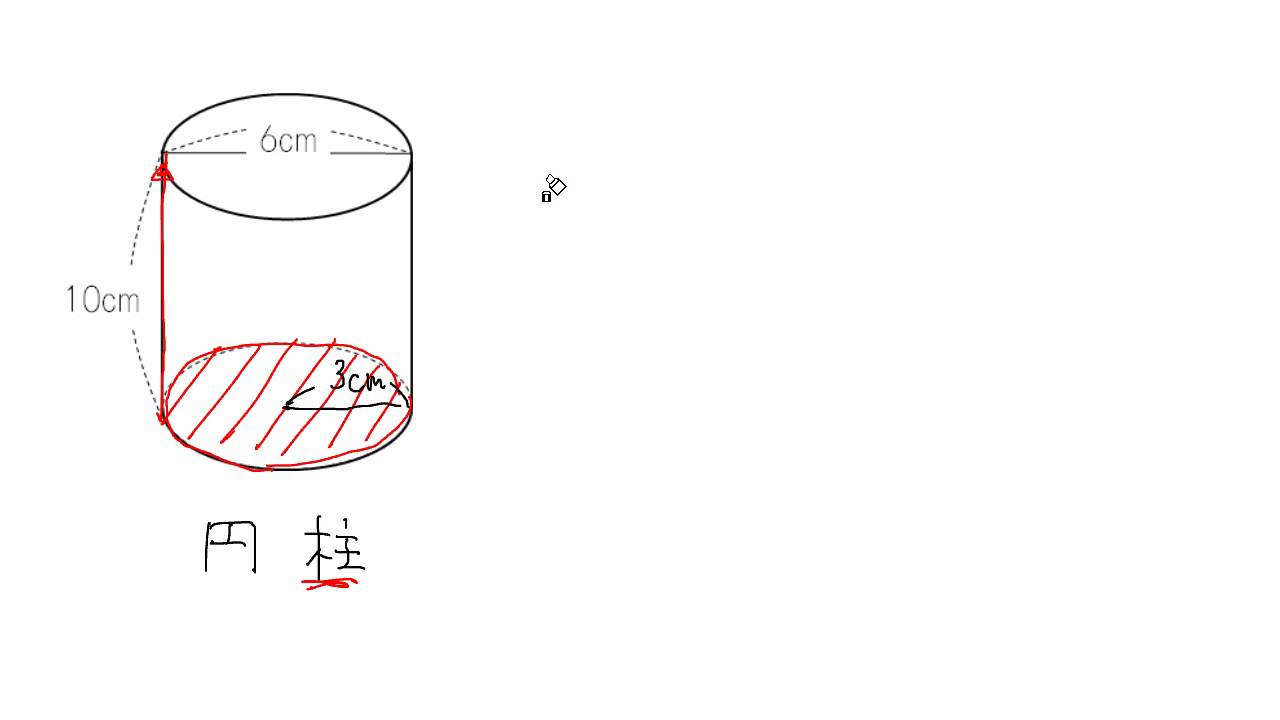


円柱の体積 Youtube
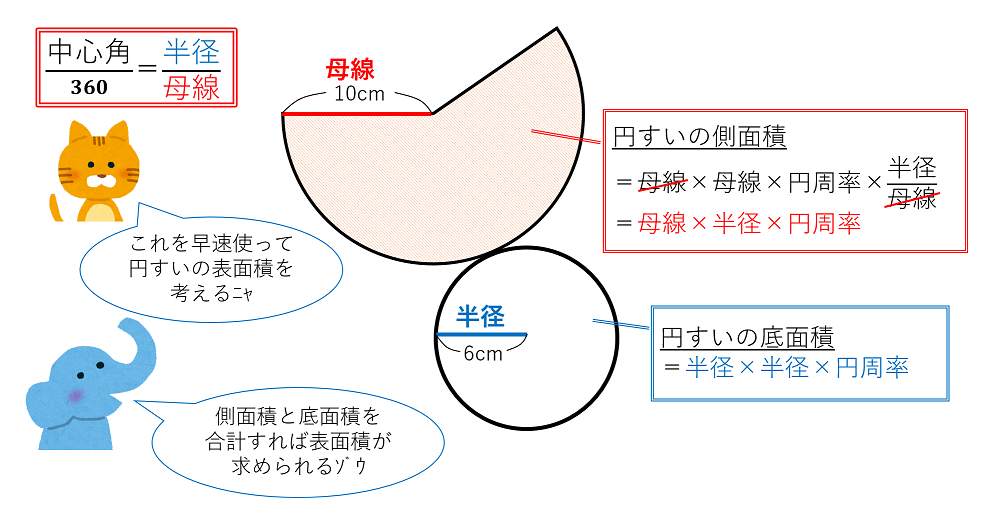


公式を図解 すい体の体積 円すいの表面積の求め方 中学受験ナビ



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



円錐の体積の求め方 公式 小学生 中学生の勉強



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
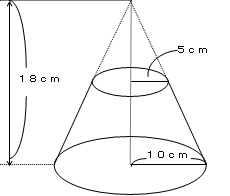


体積 円錐台の体積を求める 子供に教える算数のツボ
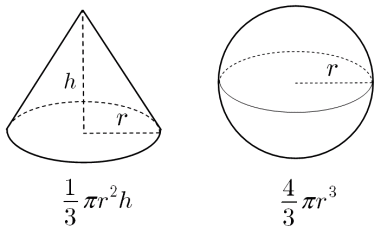


積分 体積を求める 大人が学び直す数学



円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
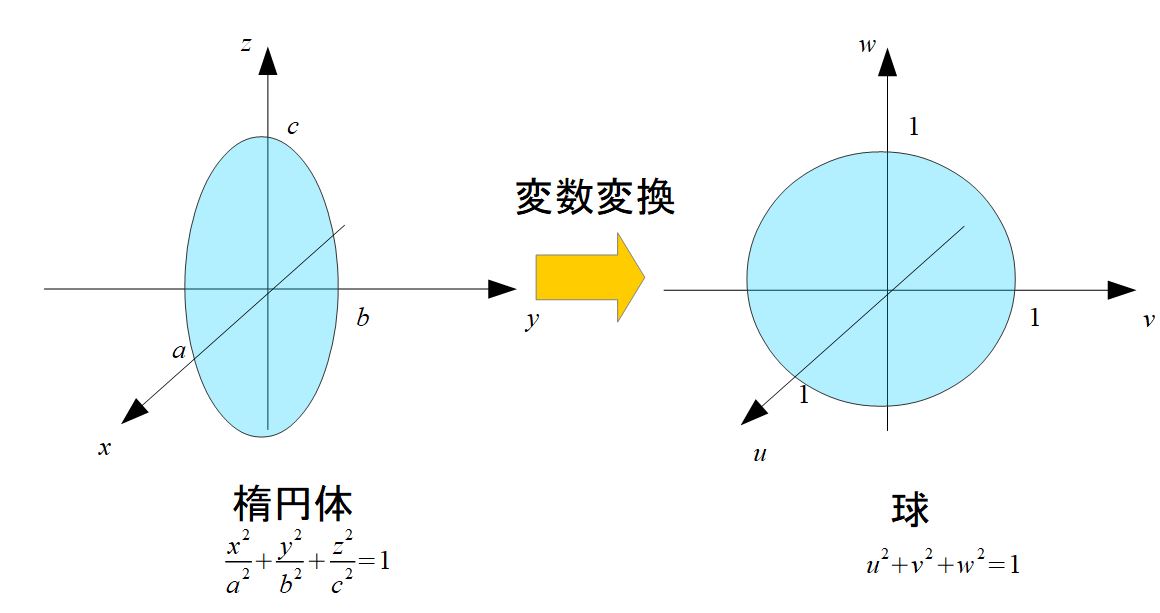


楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



立体の体積を求める公式


数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット


小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 行け 偏差値40プログラマー
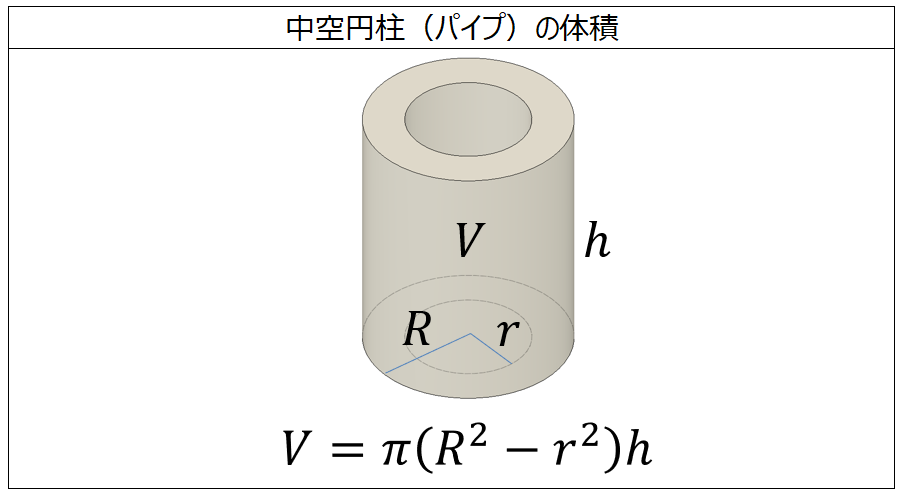


体積の計算 中空円柱 パイプ 製品設計知識



球の表面積と体積の求め方 苦手な数学を簡単に



中1 数学 6 5 球の体積 表面積 Youtube



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



球の体積 球の表面積の公式の導出 積分 優技録



球の体積と表面積 Youtube



中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
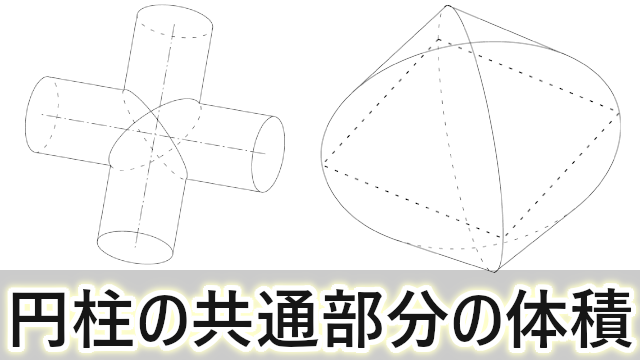


円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法



円すいのときの体積の求め方の公式と 球の体積の求め方の公式を教えてください Clear



簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ


円柱の体積の公式と性質 円の公式の使い分けなどを詳しく解説 スタモ 受験 入試 学習の総合サイト



円柱の体積の求め方 公式 小学生 中学生の勉強



中学受験 円周率暗記プリント 体積問題で間違いを連発する2つの理由 かるび勉強部屋 中学受験 勉強 暗記



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



角錐 円錐の体積と表面積の公式 数学fun



円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ
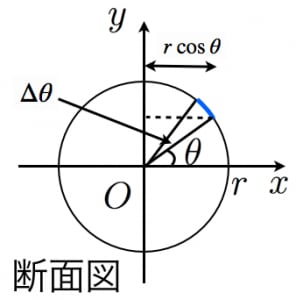


球の体積と表面積を積分で証明 高校数学の美しい物語
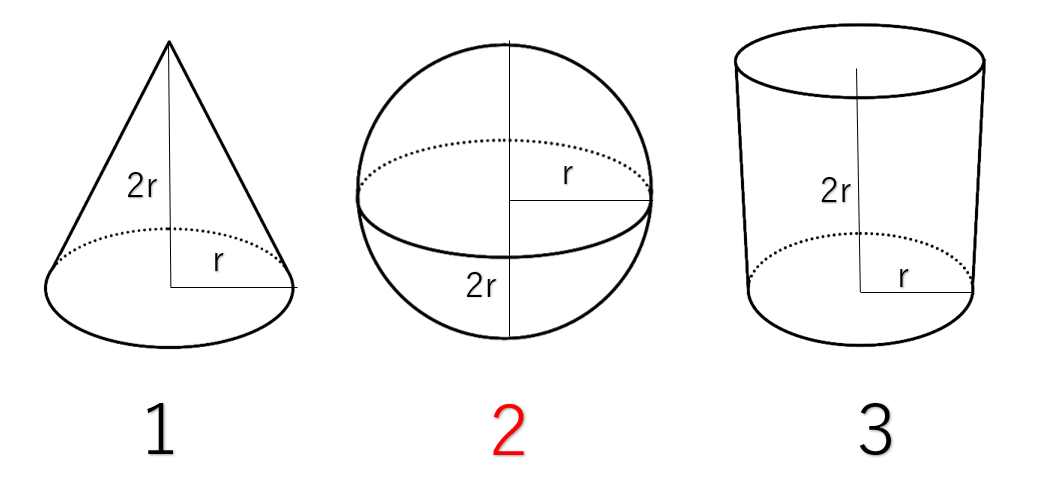


中1 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾



円柱の体積の求め方 公式と計算例



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室



球に関する公式 理数系無料オンライン学習 Kori



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ


球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス



どうして1 3なの 錐の体積の公式の求め方 まなべーと


球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス
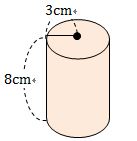


中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン


円柱の側面積は 1分でわかる求め方 公式 底面積と表面積 体積との関係


斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル



球の表面積と体積の公式 数学fun



メルカリ 小6算数 角柱と円柱の体積 問題48ページ分 スモールステップで学力アップ 参考書 444 中古や未使用のフリマ



円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
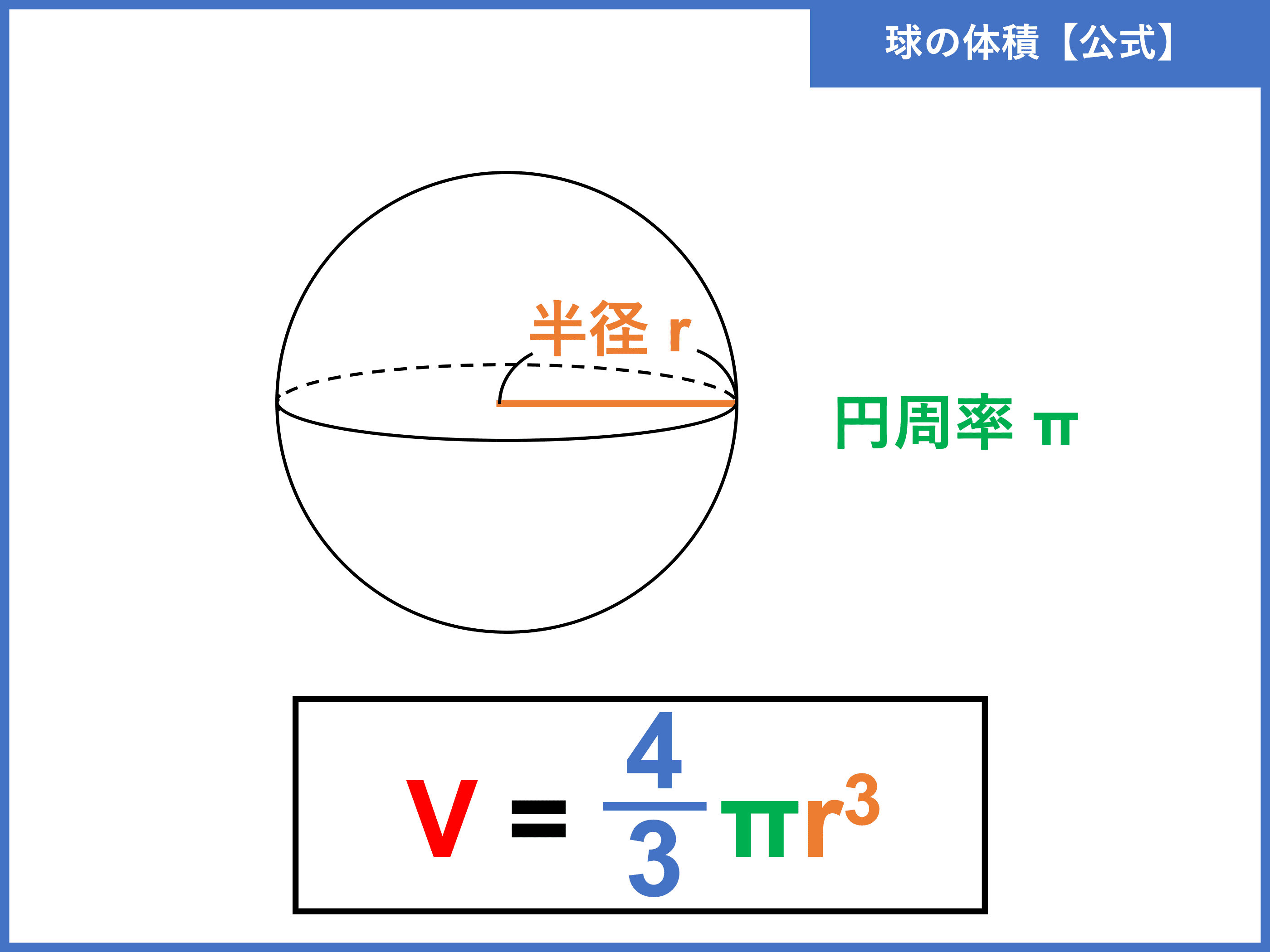


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典


円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係



丸棒の重量 円柱の体積と重量の求め方 鉄の場合
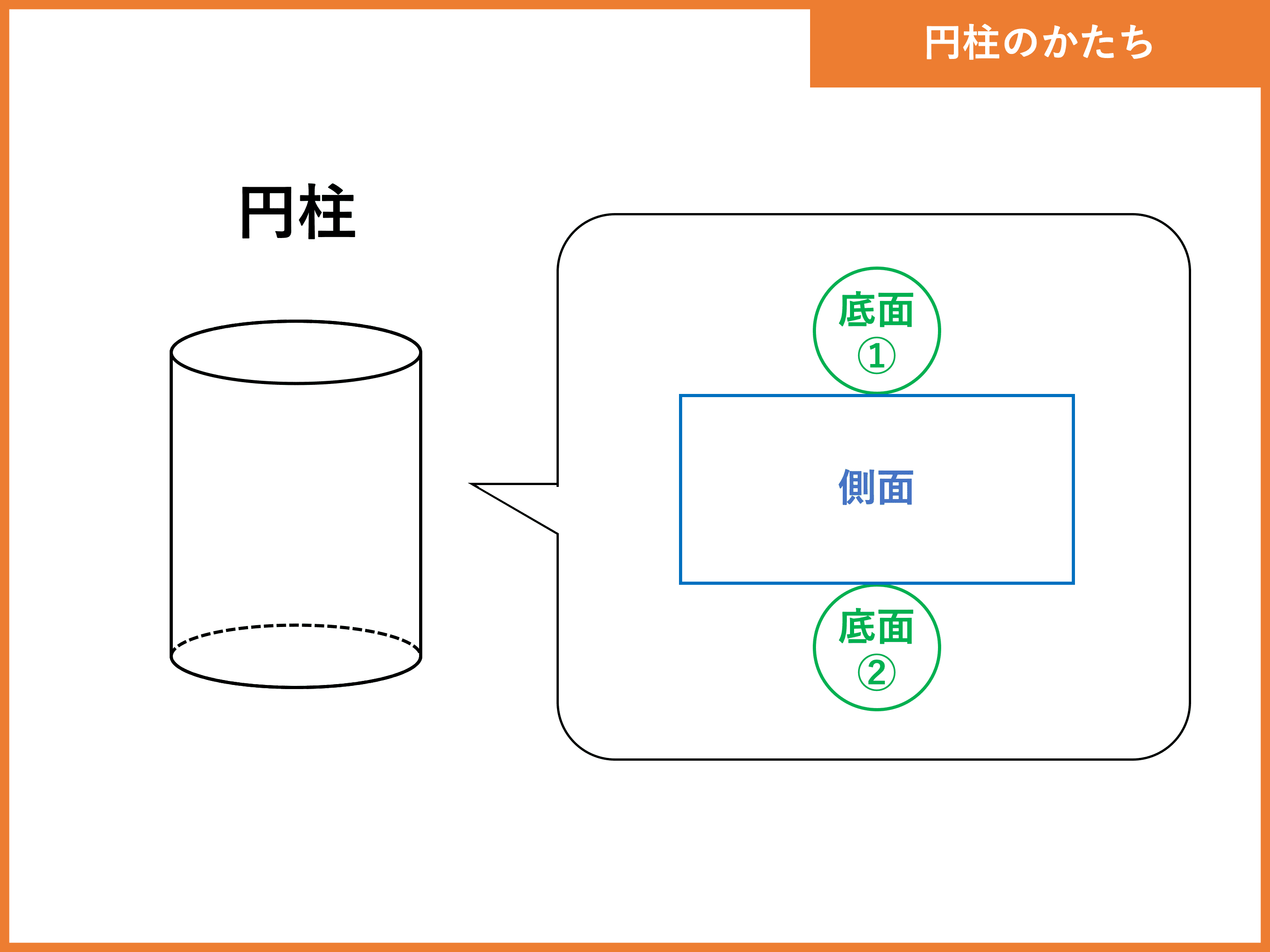


円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典



19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



円柱の表面積と体積を求める公式 具体例で学ぶ数学
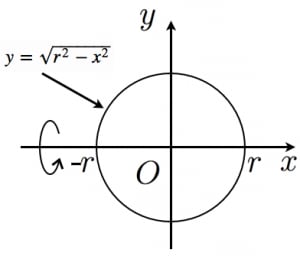


球の体積と表面積を積分で証明 高校数学の美しい物語



空間図形14 円すい台の体積 Youtube



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



球の体積と表面積 公式と計算問題と証明 Irohabook



0 件のコメント:
コメントを投稿